Scaling Up - Faster Ring Detection in CDK

In the last post I wrote on how different graph representations can affect algorithm performance. The choice of representation not only affects basic operations but can also change how an algorithm is structured. To demonstrate this I decided to take a look at ring detection in chemical structures. For this post I refer to a ring as a cycle and detection as a test that an vertex (atom) belongs to cycle of any size. I'm going to explain some concepts from the very basics but we end up with a particularly elegant (and efficient) method for cycle detection. Finally I will show how it performs when we scale up our input.

I should add there is more than one (quick) way to detect cycles, the end implementation definitely is nothing new but it was certainly fun to program.

Cycle Detection in the CDK

In the Chemistry Development Kit (CDK) the SpanningTree class is the usual choice for cycle detection. It is used to obtain a molecule (aka AtomContainer) that only contains cyclic atoms. This molecule is then tested as to whether each atom is pressent.

Code 1 - Using the existing SpanningTree

// create the spanning tree and obtain the cyclic fragments
SpanningTree   tree   = new SpanningTree(molecule);
IAtomContainer cyclic = tree.getCyclicFragmentsContainer();
 
// test whether the cyclic fragment contains each 'atom'
for(IAtom atom : molecule.atoms()){
    cyclic.contains(atom);
}

The method is relatively fast and is used in some core concepts, including, aromaticity detection and atom typing.

Depth First Target Search

I'll come back to why the spanning tree is important and what it actually is later. If we dig down in the code we find the spanning tree uses a depth first target search to test whether a vertex is in a cycle. This mirrors the core idea of a cycle in an undirected graph.

An undirected graph has a cycle if and only if a depth-first search (DFS) finds an edge that points to an already-visited vertex (a back edge) - Wikipedia

The exact piece of code which is used is a depth first target search. Lets have a look at this targeted DFS - I've restructured the code a little so it fits in the snippet, you can see the original here.

Code 2 - SpanningTree internals

// see org.openscience.cdk.PathTools.depthFirstTargetSearch for original code
boolean targetedDFS(IAtomContainer mol, IAtom atom, IAtom target, IAtomContainer path) {        
     
    atom.setFlag(VISITED, true);                                   // step 1                                           
        
    for (IBond bond : mol.getConnectedBondsList(atom)) {           // step 2            
            
        IAtom connected = bond.getConnectedAtom(atom);             // step 3
            
        if (!connected.getFlag(VISITED)) {                         // step 4 
        
            path.addAtom(connected);                               // step 5
            path.addBond(bond);                                    
                
            if (connected == target) {                             // step 6   
                return true;                  
            } else {                     
                if (targetedDFS(mol, connected, target, path)) {   // step 7
                    return true; 
                } else {            
                    path.removeAtom(connected);                    // step 8 
                    path.removeBond(bond);                         
                }
            }
        
        }
    }
        
    return false;                                                  // step 9
}

I'm going to step through each block and so it is clear what it does, I will add some commentary on various aspects after.

1. indicate we are visiting atom
2. access all bonds connected to the atom
3. for each bond from the atom get the connected atom
4. check we have not visited the connected atom - note we actually may be in the process of visiting it further up the stack
5. add the connected atom to our path
6. if the connected atom is our target return true - the path will contain all atoms we visited to get to the target
7. connected atom was not the target, recursively visit the neighbours of the connected atom and attempt to find the target. If whilst recursively visiting we found the target, return true, the path still contains all atoms which lead to the target.
8. we did not find the target whilst visiting the connected atom, connected atom cannot therefore lead to the target and we remove it from the path.
9. we have visited all connected atoms and did not find the target, return false

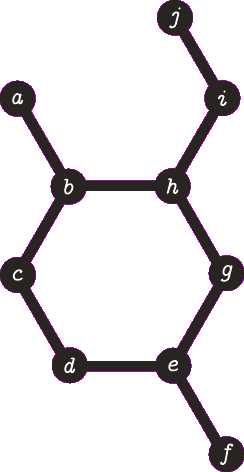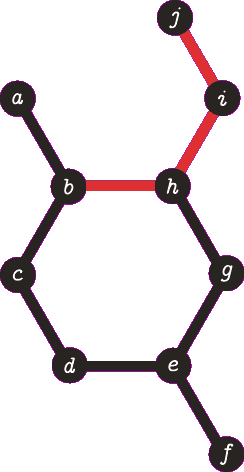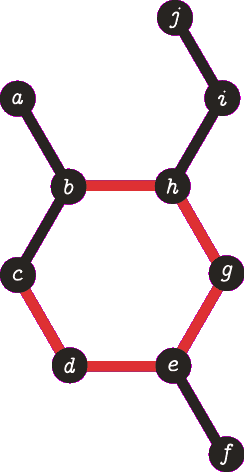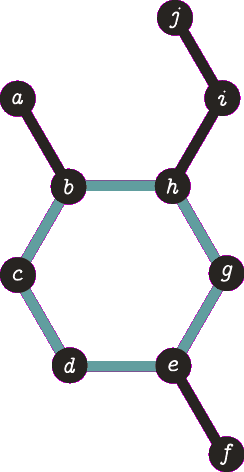
It is important to note the atom/target can not be the same atom. For the purposes of demonstration let us presume this is allowed - this will become more clear when we look back at spanning tree. The following animation visually represents a targeted DFS on the atoms a, f and b. The visit order of the neighbours is determined by the order in which the edges are stored - the animations depict the worst possible route but this of course can occur.

A DFS from vertex a, the search terminates when we visit vertex b a second time.  Vertex b was not the target, no path is returned.

A DFS from vertex f, the search terminates when we visit vertex e for the second time.  Vertex e was not the target, no path is returned. Note that we are traversing the same edges as before.

A DFS from b, the search finds the target (b) and the path of {b, h, g, e, d, c} (which are all in a cycle) is returned.

Time Complexity

There a couple of things to note about the complexity of the above process. Here I denote the number of vertices (atoms) as |V| and the number of edges (bonds) as |E|. This follows the standard Big O notation for graphs.

Firstly, the VISITED flag (step 1) needs to be reset for each subsequent search. This is a consequence of mixing the algorithm state with our data model. To re-invoke this method over the same set of atoms (which we need to do) we first need to reset all the flags. Reseting the flags takes time proportional to |V| + |E|.  Secondly, to access the connected bonds (step 2) we need to perform a linear search (in coordinate list representation) taking at most |E|. Thirdly, to remove the atom and bond (step 8) we need to again do a linear search over all atoms/bonds taking at most |V| and |E| operations respectively. Phew, thats a lot of |V|'s and |E|'s floating about. It should be noted we need to do a targeted search for every vertex (atom). This would take a very long time, surely there is a way we can reduce the number of atoms we need to test? This is exactly where the spanning tree is used.

Spanning Tree

Okay, so what is a spanning tree? I'm not a graph theorist so my definitions may be slightly loose, the links below will provide a more accurate definition. Well a tree is a connected graph where every vertices is connected by one simple path - that is, there are no cycles. A spanning tree of a graph is the transformation of the graph (which may contain cycles) into a tree which contains only enough edges to span all connected vertices. In other words it does not contain redundant edges.

Valid spanning trees of our example graph. The dashed line indicates where an edge was removed.

The spanning tree provides several interesting properties. Any edges that are not pressent in the tree are redundant and therefore much be in a cycle. If we obtain multiple trees from our graph, our graph is disconnected. The CDK uses an implementation of Kruskal's algorithm to calculate the spanning tree which runs in O(|E| log |E|).

Once the spanning tree is determined we now know which edges are in a cycle. We then use the depth first targeted search (above) between two vertices of any edges that were removed.

Depth First Target Search on a spanning tree. The operation is equivalent to the previous self target search on single vertices. Instead of the same query/target vertex we have the same query/target edge. 

This process is efficient as we only ever check targets which must be in cycles. However, If we have two or more cycles we still traverse the graph multiple times. Can we detect all cycles and only visit each edge once...?

Changing the Representation

Firstly lets use the more friendly adjacency list for traversal. As shown previously the adjacency list allows quicker access to adjacent neighbours (step 2). When we create the adjacency list we index each vertex to an int value between 0 and |V|. This index allows us to quickly access the vertex value (atom) but it also allows us to decouple the algorithm visited state by storing a boolean array of size |V|(step 1). In fact we can do even better by storing which vertices we have visited in a BitSet or if the molecule is small enough on a single 64-bit long value. Similarly as we do not need to know the order we can also store the path we visited as a BitSet (step 8).
All these changes sound great but we will still be visiting the same vertices multiple times and we still need to calculate the spanning tree. There is actually a far simpler way - which doesn't require the spanning tree at all. In truth I truncated the wikipedia quote at the start of this post. The solution should be clear from the first diagram but if not here is the full quote

An undirected graph has a cycle if and only if a depth-first search (DFS) finds an edge that points to an already-visited vertex (a back edge).  Equivalently, all the back edges, which DFS skips over, are part of cycles. In the case of undirected graphs, only O(n) time is required, since at most n − 1 edges can be tree edges (where n is the number of vertices). - Wikipedia

Here O(n) means O(|V| + |E|) - Now, that's an algorithm that scales!

The animations below demonstrated what the targeted DFS was doing and what we can actually do.

Previous target DFS from vertex a, the search terminates when we visit vertex b a second time.  Vertex b was not the target, no path is returned and no cycles were marked.

DFS from a, when b is reached for the second time all vertices we visited between now and when we first visited b can be marked as being in a cycle.

With our adjacency representation we can do this very easily. The core method of the algorithm can be written in only a few lines of code.

Code 3 - Is in ring

void check(int i, long parentPath, long path) {
 
    explored |= path = setBit(stack[i] = path, i);
 
    for (int j : graph.get(i)) {
        if (isBitSet(parentPath, j))
            rings |= stack[j] ^ path;
        else if (!isBitSet(explored, j))
            check(j, stack[i], path);
    }
}

Okay I'm cheating a bit, lets make this a bit more legible and add some comments.

Code 4 - Is in ring, verbose

// adjacency list representation
List<List<Integer>> graph;
 
// index of set bits indicate which vertices we have visited
long explored;                    
 
// index of set bits indicate the vertices in rings
long rings;
 
// keeps track of our state when we visit each vertex - each vertex is only
// visited once
long[] stack;
 
boolean isInRing(int i) {
    // check if vertex i has been explored
    if (!isBitSet(explored, i))
        check(i, 0, 0); // search from i to all connected components
    // check with the bit 'i' is set and thus in a ring
    return isBitSet(rings, i);
}
 
void check(int i, long parentPath, long path) {
 
    stack[i] = path;             // store our state before we visit 'i'
    path     = setBit(path, i);  // set 'i' is visited in out current path
    explored = explored | path;  // set 'i' as explored globally
 
    // for each neighbour of i
    for (int j : graph.get(i)) {
 
        // have we visited it before in out parent path?
        // - we use the parent path as one 'j' will be our
        //   parent and this would falsely indiciate a cycle.
        if (isBitSet(parentPath, j)) 
        
             // take the different between our current path and our state
             // right before we last visited 'j'. this difference is the
             // set of vertices we traversed to reach 'j' again. mark all
             // of these as in a cycle/ring. 
            rings |= stack[j] ^ path;
 
        // have we explored j? stops us revisiting parent vertices
        else if (!isBitSet(explored, j))
            // check vertex 'j' passing the path before we
            // visited 'i' as the parent path and our current path
            check(j, stack[i], path);
    }
}

Benchmark

To benchmark this I wrote a quick executable jar that takes an input SDF and tests how long it takes to find all the ring atoms. It prints out the answer from each method to confirm they performed correctly. It also includes a stress test which I'll come back to in a bit. The source code and cycle-detection.jar can be found on github project. Here is an example usage (--help will print all options):

Code 5 - Runnable benchmark example

java -Xmx1G -jar cycle-detection.jar -i ~/Downloads/Compound_000000001_000025000.sdf

The times change a little but normally the BasicRingTester is about 800% to 1000% faster than the spanning tree. For 20,000 molecules the BasicRingTester usually takes about 120-190 ms and the SpanningTree takes between 900-1000 ms to complete.

Average (n=50) time taken to detect vertices which belong to cycles in PubChem Compound ID 00001-25000

I mentioned in the last post there is some overhead in converting our graph to the adjacency list. We can test how much this overhead is by removing the actual ring computation. This can be done by setting the simulate option.

Code 6 - Runnable benchmark example 2

java -Xmx1G -jar cycle-detection.jar -i ~/Downloads/Compound_000000001_000025000.sdf --simulate

If this option is set we'll see that is takes 90-110 ms (on my test input) just to convert the actual graph and the true time of the computation is very quick at around 20-50 ms. We can show just how quick the algorithm is if we scale up the input and perform the stress test.

The stress test loads a graphene molecule with 2,598 atoms in cycles and a single atom which is not.

Molecule loaded for stress testing

It we run the benchmark we find the BasicRingTester runs in a couple of milliseconds while the SpanningTree can take up to and over a minute.

Average (n=5) time taken todetect vertices which belong to cycles in a graphene molecule with ~2,500 atoms

To run the stress test, yourself

Code 7 - Runnable benchmark example 3

java -Xmx1G -jar cycle-detection.jar --stress-test -i dummy

Final Thoughts

Although the above code is just for a boolean test (i.e. is this atom in a ring) this is still very useful. The simple calculation in the CDKHuckelAromaticityDetector use the spanning tree to simply get which atoms are in a ring system. Clearly it is possible to adapt the code to detect the independent systems. The technique also roughly preserves the concepts of a path it may well be possible to determine other cycle properties (i.e. size) just by looking at the sets of vertices as they are discovered.

Edit: added graphs to better demonstrate the performance of each method

Edit: this is now available using org.openscience.cdk.ringsearch.RingSearch.